
It has been a very long time since my last post. I have been quite busy in last 7 years.
Last year, (Before this COVID-19 pandemic) I took some time to develop a pH meter for swimming pools using easy to get and low cost components.
One of the most important parameters to monitor and control in a swimming pool is the pH. Normally this is keep in a range between 7.2 and 7.6.
There are various methods to measure the pH in the swimming pool; the most commons are chemical titration and paper strips. Also there are digital meter at low cost.
Last year, (Before this COVID-19 pandemic) I took some time to develop a pH meter for swimming pools using easy to get and low cost components.
One of the most important parameters to monitor and control in a swimming pool is the pH. Normally this is keep in a range between 7.2 and 7.6.
There are various methods to measure the pH in the swimming pool; the most commons are chemical titration and paper strips. Also there are digital meter at low cost.

The intention of this post is not to guide you on what you should select to measure pH in your swimming pool but to show how to spend some time developing something fun and useful at last.
The idea is (or was) to develop a device that measures the pH and sends a report that can be seen on the internet. It sounds difficult but I was able to do it, so should not be that difficult!.
The idea is (or was) to develop a device that measures the pH and sends a report that can be seen on the internet. It sounds difficult but I was able to do it, so should not be that difficult!.
What we need.
To build the pH meter we use the following components.
I have never soldered any circuit in my life, so this was an opportunity to learn it. Thanks to a brother in my congregation that had the patience to help me and teach me. It can be frustrating at the beginning but later is real fun!!. So, you will need to use a soldering kit.
Other things you need
You need a computer (desktop or laptop) with an USB port to compile and upload the code in the Arduino. Also need the Arduino Programming IDE (Can download fee from the Arduino web page)
This device sends a log of the values to a FTP site. So, you will need to have your FTP site where the Arduino can connect and upload the log.
The Circuit.
In order to finally get the required circuit connected, I have gone through various trial and error… so, I will give the final sketches (this will save you a lot of time). Below are the diagrams or tips to connect the various components.
A. LCD Display
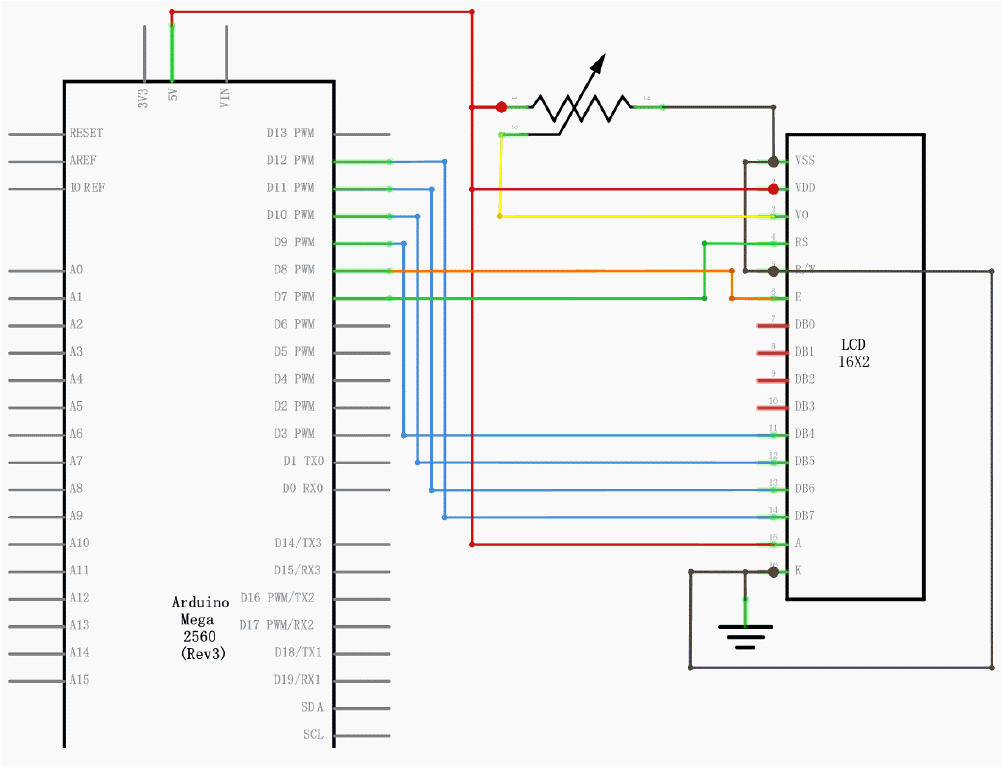
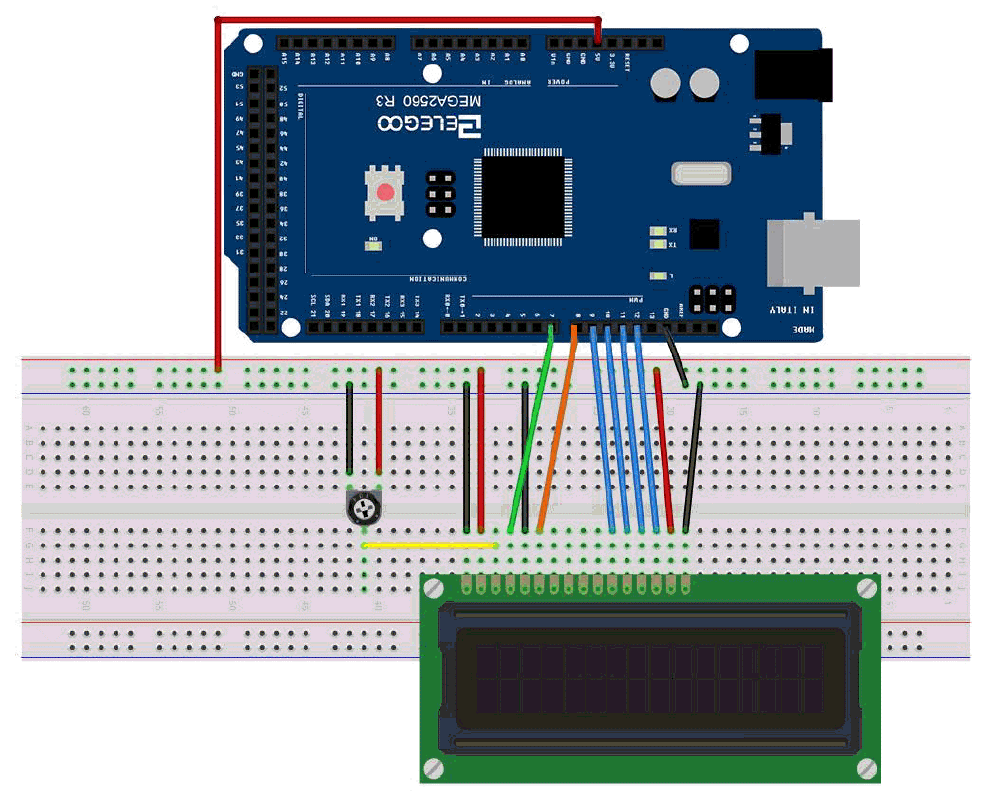
The more difficult part is to wire the LCD Display, the following diagram should help:
To build the pH meter we use the following components.
- Arduino (I used Arduino Mega 2560 controller board) with power supply. Controls all the components and run the software
- PH Value Detection Sensor Module Monitoring Control with BNC Electrode Probe – This measure the pH.
- LCD Display (LCD 1606 Module – with pin header). Displays measured values.
- DS3231 RTC Module. Provides real time clock.
- Micro SD TF Card Adapter Reader Module 6Pin SPI Interface Driver Module. This logs values and keep in a Micro SD Card
- Micro SDCard (16GB or less is ok) – Keeps the log of values.
- DS18B20 Waterproof Temperature Sensor – I added temperature measurement to the device. Added 2, one for ambient one for water temperature.
- ESP8266 ESP-01S WiFi Serial Transceiver Module with 1MB Flash – This gives internet connectivity.
- 10K Potentiometer – to adjust LCD Brightness
- PCB Perforated Printed Circuits Boards, push buttons, resistors and cables of different colors. I used Stranded Wire 24 AWG.
I have never soldered any circuit in my life, so this was an opportunity to learn it. Thanks to a brother in my congregation that had the patience to help me and teach me. It can be frustrating at the beginning but later is real fun!!. So, you will need to use a soldering kit.
Other things you need
You need a computer (desktop or laptop) with an USB port to compile and upload the code in the Arduino. Also need the Arduino Programming IDE (Can download fee from the Arduino web page)
This device sends a log of the values to a FTP site. So, you will need to have your FTP site where the Arduino can connect and upload the log.
The Circuit.
In order to finally get the required circuit connected, I have gone through various trial and error… so, I will give the final sketches (this will save you a lot of time). Below are the diagrams or tips to connect the various components.
A. LCD Display
The more difficult part is to wire the LCD Display, the following diagram should help:
A more realistic view using a “Bread-board” is:
B. Push button
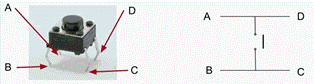
Push button connection is quite easy; 5 Volts need to be supplied to the button input and the output needs to be wired to the Digital Pin 3.
Please note that most common push button has 4 “legs”, for two inputs and 2 outputs, both inputs are connected and both output are also connected. So, you need to identify with pair can be input and which can be output.
Following the figure of the button you need to supply 5V to let A (or D) and wire leg B (or C) to Digital pin 3.
During operation the button need to be hold-down for at least 2 seconds for change in displayed variable to take effect.
Push button connection is quite easy; 5 Volts need to be supplied to the button input and the output needs to be wired to the Digital Pin 3.
Please note that most common push button has 4 “legs”, for two inputs and 2 outputs, both inputs are connected and both output are also connected. So, you need to identify with pair can be input and which can be output.
Following the figure of the button you need to supply 5V to let A (or D) and wire leg B (or C) to Digital pin 3.
During operation the button need to be hold-down for at least 2 seconds for change in displayed variable to take effect.

C. The pH Sensor Module and probe.
For the pH Sensor mole we need to supply 5V and ground to two pins as shown in the figure.
The PO pin needs to be wired to the Analog Pin A0 of the Arduino. This will send a voltage signal that will be converted to a value between 0 – 1023.
The DO and the TO pins are not being used by the code but these can be used for Alarm and Temperature reading.
The screw on top of the blue box closer to the BNC connector is the one we use when we need to adjust or zero-calibrate the module.
For the pH Sensor mole we need to supply 5V and ground to two pins as shown in the figure.
The PO pin needs to be wired to the Analog Pin A0 of the Arduino. This will send a voltage signal that will be converted to a value between 0 – 1023.
The DO and the TO pins are not being used by the code but these can be used for Alarm and Temperature reading.
The screw on top of the blue box closer to the BNC connector is the one we use when we need to adjust or zero-calibrate the module.
D. Temperature Sensors
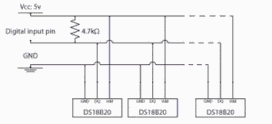
Both Temperature sensors need to be connected as show in the figure. Common 5V and ground need to be provided.
Also, the circuit requires a 4.7 Ohm resistor wired from the 5V supply to the Digital Signal from the Temperature sensors. This wire after the resistor needs to be connected to the Digital Pin 2 of the Arduino.
Both Temperature sensors need to be connected as show in the figure. Common 5V and ground need to be provided.
Also, the circuit requires a 4.7 Ohm resistor wired from the 5V supply to the Digital Signal from the Temperature sensors. This wire after the resistor needs to be connected to the Digital Pin 2 of the Arduino.

E. DS3231 RTC Module (Real time clock).
The connection of the RTC is quite simple, need to provide 5V and Ground to the respective pins. The SDA needs to be wired to the SDA pin in Arduino and the SCL to the SCL pin in the Arduino. Also need to provide the required battery.
The connection of the RTC is quite simple, need to provide 5V and Ground to the respective pins. The SDA needs to be wired to the SDA pin in Arduino and the SCL to the SCL pin in the Arduino. Also need to provide the required battery.

F. Micro SDCard Module
Need to supply 5V and Ground to the Micro SDCard. The rest of pin need to be connected as follows:
MOSI to pin 50
MISO to pin 51
CLK to pin 52
CS to pin 53
Need to supply 5V and Ground to the Micro SDCard. The rest of pin need to be connected as follows:
MOSI to pin 50
MISO to pin 51
CLK to pin 52
CS to pin 53
G. ESP8266 ESP-01 WiFi Serial Transceiver Module
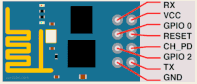
Connect as follows:
RX — TX 1 (Pin 18)
TX — RX 1 (Pin 19)
GND — GND
GPIO 0 - GND
VCC – 3.3V
CH_PD – 3.3V
It is very important to connect to 3.3 Volts supply. 5V will damage the ESP8266 Module.
Connect as follows:
RX — TX 1 (Pin 18)
TX — RX 1 (Pin 19)
GND — GND
GPIO 0 - GND
VCC – 3.3V
CH_PD – 3.3V
It is very important to connect to 3.3 Volts supply. 5V will damage the ESP8266 Module.

The Code
Download the code from the following link:
pHmonitorCode.txt
Note that you will need to install some libraries. I have placed those libraries in zip file downloadable from the following links:
Arduino-Temperature-Control-Library-master.zip
ESP8266wifi-master.zip
OneWire-2.3.4.zip
Timermaster.zip
Once you download them you can install them following the instruction to import zip libraries in Arduino IDE.
You need to customize several code lines. In lines 30 to 34 and 439, 440, 444 you need to type the information required for your wifi connection and your FTP server.
Now you are ready to compile the code and upload it in the Arduino.
It is important to set the process clock right, likely the DS3231 RTC Module will be out of time/date. To set the time of the clock you need to “uncomment” line 87 (removing the characters //) so that when compiling and running the code for first time the clock will be set to the current compiling time. After doing this, you need to set line 87 back as comment code (adding again //) and compile/run the program so that the time is not reset anymore. The DS3231 will keep the time from now on. Any time you need to set the time of the device you will need to follow the steps described in this paragraph.
How does this work?
You probably can find better way to “wrap” these device. I used a plastic container and put all circuits inside. As this will likely be installed outdoor proper protection to avoid ingress of water or moisture must be considered.
This device will read the pH and 2 temperatures (one can be ambient temperature the other the water temperature).
The push button is used to change what is shown in the LCD display. By default should the last 5 readings of pH. By pressing the bush button you then can display:
The code is set to take pH reading every 3 minutes and send a report to the FTP site every 30 minutes. You can change that by tweaking lines 46 and 48 in the code.
An example of the report can be seen at:
www.alexmichinel.com/Pooldata/SHORTLOG.TXT
You can make it more elaborated by modifying the code… The sky is the limit!!
- Temperature sensor 1 in oC and oF
- Temperature sensor 2 in oC and oF
- pH Values (default at startup – Displays last 5 values)
- pH sensor (Raw data from the sensor a number between 0 and 1023 related to the voltage)
- File size (Log size in bytes)
- Wifi Status (Ok or NA – for Not Available)
The code is set to take pH reading every 3 minutes and send a report to the FTP site every 30 minutes. You can change that by tweaking lines 46 and 48 in the code.
An example of the report can be seen at:
www.alexmichinel.com/Pooldata/SHORTLOG.TXT
You can make it more elaborated by modifying the code… The sky is the limit!!

Calibration
Likely you need to calibrate the pH sensor. There are two type of calibration, the zero and the range.
The zero calibration is done by carefully turning the screw in the pH control module (Scree is located on top of the blue box closer to the BNC connector). The idea is to have a reading of 7pH (or about 521 raw sensor reading) when there is 0 Voltage from the sensor. This can be achieve by jumping the core wire and the shield in the BNC connector of the pH controller module and moving the proper screw to get about 521 raw count from the sensor.
For the range calibration you prepare solutions with known pH. I prefer to use pH calibration Buffer Powder. Prepare solutions for 9.18 and 6.86 and find the lineal relation between the Raw pH value from sensor and the pH. The slop and the bias of the lineal relationship can be input in the code in lines 60 and 61 (variables mVal and bVal)
Conclusion
All this may sound complex… but it is really fun and entertaining. Requires patience and determination to complete the task!! You can surely do it too!!
There are many references and links in the internet that can help you in every step of the way.
References:
Arduino Web page (www.arduino.cc)
Likely you need to calibrate the pH sensor. There are two type of calibration, the zero and the range.
The zero calibration is done by carefully turning the screw in the pH control module (Scree is located on top of the blue box closer to the BNC connector). The idea is to have a reading of 7pH (or about 521 raw sensor reading) when there is 0 Voltage from the sensor. This can be achieve by jumping the core wire and the shield in the BNC connector of the pH controller module and moving the proper screw to get about 521 raw count from the sensor.
For the range calibration you prepare solutions with known pH. I prefer to use pH calibration Buffer Powder. Prepare solutions for 9.18 and 6.86 and find the lineal relation between the Raw pH value from sensor and the pH. The slop and the bias of the lineal relationship can be input in the code in lines 60 and 61 (variables mVal and bVal)
Conclusion
All this may sound complex… but it is really fun and entertaining. Requires patience and determination to complete the task!! You can surely do it too!!
There are many references and links in the internet that can help you in every step of the way.
References:
Arduino Web page (www.arduino.cc)



 RSS Feed
RSS Feed